We recently received this question from a visualization major…
We use the New Munsell Student Color Set in our color theory course. In the chapter about color harmony, Munsell shows us a few 3-dimensional theories to create a balanced color palette, but unlike the other types of harmonious color balance, no examples are provided. Have these theories, such as the conical spiral, been made into compositions and palettes before? We asked Theresa-Marie Rhyne, an expert in the field, to give the answer.
Color Attributes
When Albert Henry Munsell set out to create his color space in 1898, he was seeking a
system that had a meaningful notation of color that stepped beyond the use of color
names that he determined to be misleading. He organized colors by defining the
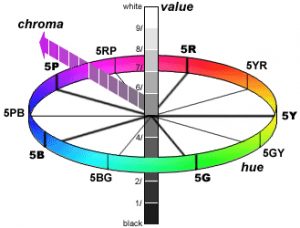
concepts of hue, value and chroma for an individual color, In Figure #1, we show a
diagram of the Hue, Value and Chroma attributes, adapted from Munsell’s original work.
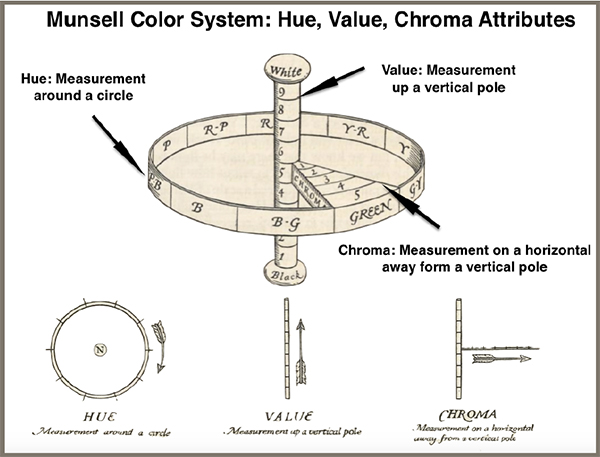
Figure #1: Combined illustrations of the Munsell Color System: Hue, Vlue, Chroma Attributes from Cleland, T.M. et al., A Grammar of Color Arrangements of Strathmore Papers in a Variety of Printed Color Combintations According to the Munsell Color System, Strathmore Paper, Co., Mittineague, MA, 1921 (public domain) Text annotations added by Theresa-Marie Rhyne, 2015.
Visualizing Color Attributes
It was Munsell’s hope that a three dimensional sphere could be developed from these
three attributes that would allow for cross sections that could be used in various ways
such as color harmony explorations. Munsell was able to create visually uniform
distances between colors due to his extensive testing of the human visual response to
color. Unfortunately, his studies indicated that it was not possible to create a three
dimensional color sphere due to unequal numbers of chroma values among hues. As
shown in Figure #2, one hue might have a total of 18 chroma values, while another
might have 6. As a result, Munsell abandoned the three dimensional sphere concept for
a Munsell Color Tree concept.
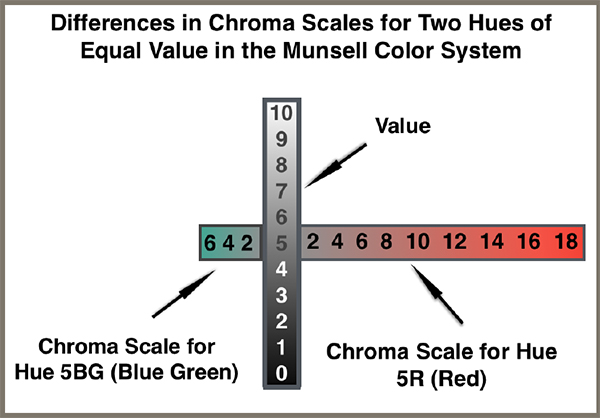
Figure #2: Differences in Chroma Scales for Two Hues of Equal Value in the Munsell
Color System. Illustration by Theresa-Marie Rhyne, Copyright 2015.
The Conical Spiral & Color Harmony
It is possible to use computer graphics rendering methods to create a three dimensional
conical spiral that connects the elements of the Munsell Color Tree into a surface. The
three dimensional conical spiral could certainly be sliced and diced to suggest color
relationships like color harmony. However, the original Munsell Color Order System
does not have defined mathematical relationships to specify the conical spiral surface
and thus support the accuracy of the color relationships. Since the Munsell Color Order
System is over one hundred years old, there is no doubt that someone has evolved their
own three dimensional conical spiral that is sliced and diced to present color
relationships.
Thank you for the terrific question, Sincerely, Theresa-Marie Rhyne
About the Author
Theresa-Marie Rhyne is an expert in the field of computer-generated visualization and a consultant who specializes in applying artistic color theories to visualization and digital media.
She has consulted with the Stanford University Visualization Group on a color suggestion prototype system, the Center for Visualization at the University of California at Davis and the Scientific Computing and Imaging Institute at the University of Utah on applying color theory to ensemble data visualization. She is the author of the book: “Applying Color Theory to Digital Media and Visualization” from CRC Press.
I found the Munsell Colour system confusing.
It is the only system that has 10 units instead of 9 hence the mid value is 5 & 6 rather than 5. Also the numbering is the reverse of every other value scale I have seen or been taught.
Having 10 colour separations does not make sense to me.
If you start with 3 primary colours, add the secondary colours between them you get 6 colours. Adding the tertiary colours gives you 12 colours. This makes a lot more sense to me rather than Munsell’s colour wheel with 10 colours.
As mentioned here, it is over one hundred years old and the art world has moved on since then.
Thank you for your comment.
Indeed, you are correct that Munsell Hues are defined by 10 divisions: Red (R), Red Yellow (RY), Yellow (Y), Green Yellow (GY), Green (G), Blue Green (BG), Blue (B), Purple Blue (PB), Purple (P) and Red Purple (RP).
Munsell considered 10 divisions for hues to be more effective than the pre-existing Red Yellow Blue (RYB) painters color model.
From your comments, I gather your preference is for a 3 hue primary color model. 3 primary color models existed before the Munsell Color System and can be found in the writings of Michel-Eugene Chevreul among many others.
In 1839, Chevreul published his classic color theory text entitled “The Law of Simultaneous Color Contrast” that included Chevreul’s hemispherical color model of Primary (Red, Yellow and Blue) hues and Secondary (Orange, Green and Violet) hues.
Munsell was aware of the Chevreul hemispherical color model and chose to develop a 10 divisions model instead. As noted earlier, the Munsell hues are specified as: Red (R), Red Yellow (RY), Yellow (Y), Green Yellow (GY), Green (G), Blue Green (BG), Blue (B), Purple Blue (PB), Purple (P) and Red Purple (RP).
I can t understand how is made a red scale ? Shall I mix white and black ( grey scale ) in red or mix several colours like white, yelllow, blue and violet?